PASCAL ÜÇGENİ

Pascal Üçgeni (Pascal Triangle)


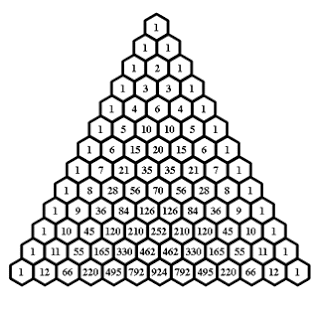Pascal üçgenindeki sayılar kendi üstündeki sayıların toplanarak yazılmasıyla elde edilir. Bu arada her satırın başına ve sonuna 1 yazılır.
Hakkında:
Pascal üçgeni olarak bilinen, bu üçgen ile ilgili Pascal’ dan öncede çalışmalar yapılmıştır. Çinli bilim adamlarından Pingala, Müslüman bilim adamlarından Ömer Hayyam gibi bir çok bilgin bu üçgen üzerinde incelemeler yapmıştır. Blaise Pascal ise kendinden önceki çalışmaları toplayıp farklı alanlarda ki uygulamalarını keşfetmiştir. Uygulama alanları içinde Olasılık, Alt küme hesabı, İki terimli bir harfli ifadenin kuvvetlerinin hesabı gibi farklı kullanım alanları vardır.
Bazılarını inceleyelim;
Altküme sayısı hesaplarken Pascal üçgenini kullanabilirsiniz.
B={a,b,c,d} B kümesi 4 elemanlıdır. [s(B)=4] Bu kümenin alt kümeleri Pascal üçgeninin 1..4..6..4..1 dizilişinde gizlidir.

Şöyle ki; B kümesinin
0 Elemanlı alt kümelerinin sayısı: 1 dir.
1 Elemanlı alt kümelerinin sayısı: 4 dür.
2 Elemanlı alt kümelerinin sayısı: 6 dır.
3 Elemanlı alt kümelerinin sayısı: 4 dür.
4 Elemanlı alt kümelerinin sayısı: 1 dir.

İki terimli bir harfli ifadenin kuvvetlerinin açılımındaki kat sayılar Pascal üçgeninde gizlidir.
Örneğin:




Bunun dışında faklı birkaç bilgi verelim.
Pembe çizgi üzerindeki sayılar 0 hariç doğal sayılardır.
Mavi çizgi üzerindeki sayılar Üçgen sayılardır. (Çokgensel sayılara bakın)
Aynı yöndeki sayıların toplamı(yeşil çizgileri takip edin), seçtiğimiz son sayının ters yönündeki sayıya eşittir. (Örnek: 1+2+3+4+5+6+7=28, 1+4+10+20+35=70 gibi)
Pascal üçgenindeki her satırın toplamı 2 nin kuvvetlerini verir.

Paylaşım için teşekkürler.